一、四种常用的数制及它们之间的相互转换
| 进制 | 基数 | 基数个数 | 权 | 进数规律 |
|---|---|---|---|---|
| 十进制 | 0、1、2、3、4、5、6、7、8、9 | 10 | 逢十进一 | |
| 二进制 | 0、1 | 2 | 逢二进一 | |
| 八进制 | 0、1、2、3、4、5、6、7 | 8 | 逢八进一 | |
| 十六进制 | 0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F | 16 | 逢十六进一 |
PS:
数制:计数的方法,指用一组固定的符号和统一的规则来表示数值的方法
数位:指数字符号在一个数中所处的位置
基数:指在某种进位计数制中,数位上所能使用的数字符号的个数
位权:指在某种进位计数制中,数位所代表的大小,即处在某一位上的“1”所表示的数值的大小。
十进制数转换为二进制数、八进制数、十六进制数的方法: 短除反取余法
二进制数、八进制数、十六进制数转换为十进制数的方法: 按权展开求和法
1. 二进制与十进制间的相互转换
(1)二进制转十进制
方法:“按权展开求和”
例:
规律:个位上的数字的次数是0,十位上的数字的次数是1,......,依奖递增,而十分位的数字的次数是-1,百分位上数字的次数是-2,......,依次递减。
注意:不是任何一个十进制小数都能转换成有限位的二进制数。
(2)十进制转二进制
- 十进制整数转二进制数方法:“除以2取余,逆序排列”(短除反取余法)
例:
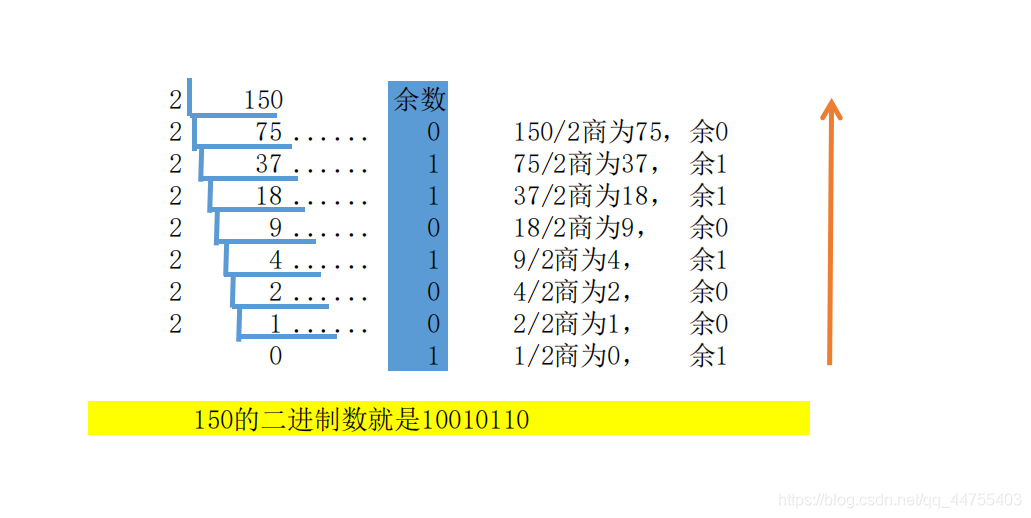
- 十进制小数转二进制小数:“乘以2取整,顺序排列”(乘2取整法)
例:

2.八进制与二进制的相互转换:
(1) 二进制数转换成八进制数:从小数点开始,整数部分向左、小数部分向右,每3位为一组用一位八进制数的数字表示,不足3位的要用“0”补足3位,就得到一个八进制数。
例:将八进制的37.416转换成二进制数:
| 数字 | |||||
|---|---|---|---|---|---|
| 3 | 7 | . | 4 | 1 | 6 |
| 011 | 111 | 100 | 001 | 110 | |
即:
(2)八进制数转换成二进制数:把每一个八进制数转换成3位的二进制数,就得到一个二进制数。
例:将二进制的10110.0011 转换成八进制:
| 数字 | ||||
|---|---|---|---|---|
| 010 | 110 | . | 001 | 100 |
| 2 | 6 | 1 | 4 | |
即:
3.十六进制与二进制的转换:
(1) 二进制数转换成十六进制数:从小数点开始,整数部分向左、小数部分向右,每4位为一组用一位十六进制数的数字表示,不足4位的要用“0”补足4位,就得到一个十六进制数。
例:将十六进制数5DF.9 转换成二进制:
| 数字 | ||||
|---|---|---|---|---|
| 5 | D | F | . | 9 |
| 0101 | 1101 | 1111 | 1001 | |
即:
(2) 十六进制数转换成二进制数:把每一个八进制数转换成4位的二进制数,就得到一个二进制数。
| 数字 | ||||
|---|---|---|---|---|
| 0110 | 0001 | . | 1110 | |
| 6 | 1 | E | ||
即:
注意:以上所说的二进制数均是无符号的数。这些数的范围如下表:
| 无符号位二进制数位数 | 数值范围 | 十六进制范围表示法 |
|---|---|---|
| 8位二进制数 | 0 ~ 255() | 00 ~ 0FFH |
| 16位二进制数 | 0 ~ 65535 () | 0000H ~ 0FFFFH |
| 32位二进制数 | 0 ~ | 00000000H ~ 0FFFFFFFFH |
二、 带符号数的机器码表示方法
1. 带符号二进制数的表示方法
带符号二进制数用最高位的一位数来表示符号:0表示正,1表示负。
| 含符号位二进制数位数 | 数值范围 | 十六进制范围表示法 |
|---|---|---|
| 8位二进制数 | -128 ~ +127 | 80H ~ 7FH |
| 16位二进制数 | -32768 ~ +32767 ) | 8000H ~ 7FFFH |
| 32位二进制数 | -2147483648 ~ +2147483647 | 80000000H ~ 7FFFFFFFH |
2. 符号位的表示:最常用的表示方法有原码、反码和补码(非常重要)


